Catalan Numbers

Before jumping to this topic, lets take a popular problem :

The Handshake Problem

We have N persons sitting on a round table. Any person can do a handshake with any other person.

    1
2        3
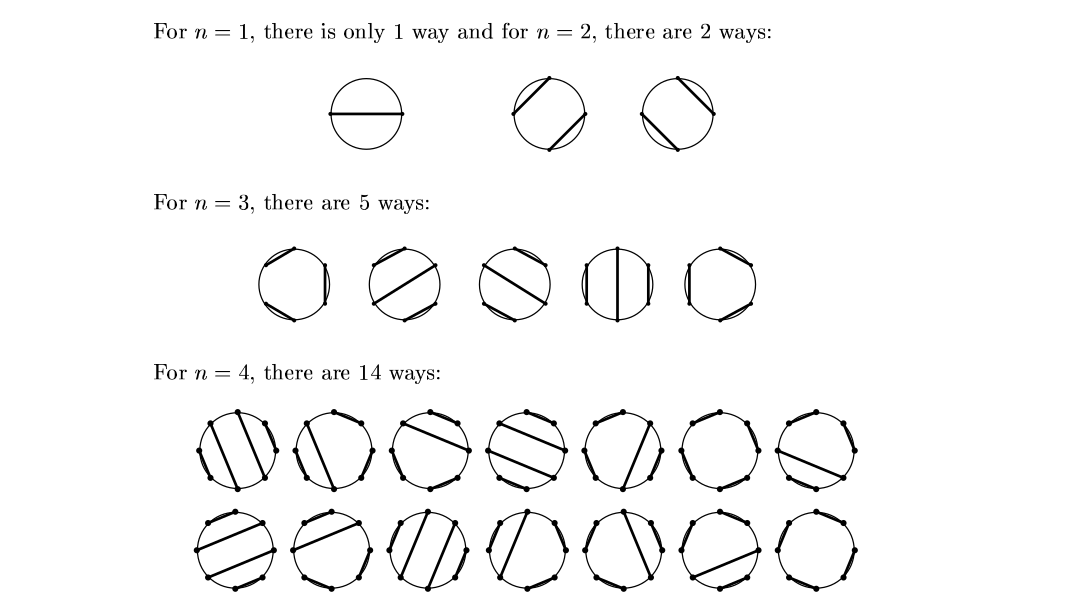
    4

Handshake with 2-3 and 1-4 will cause cross. In how many ways these N people can make handshakes so that no two handshakes crosses each other. N would be even. 

For example, in above diagram, there are two non-crossing ways to handshake {{1, 2}, {3, 4}} and {{1, 3}, {2, 4}}.

Or we can say : 

There are 2n people sitting on a round table. In how many ways can they shake their hands, in pairs, without crossing the hands?

Lets collect data for n=1, n=2, n=3,.....

So, we got a sequence of numbers i.e 1, 2, 5, 14 ..... 

& famous Recurrence relation for them is :

                                           Cn+1​ = C0​Cn​ + C1​Cn−1​ + ⋯ + Cn​C0​ = k=0∑n​Ck ​Cn−k​

These are the Catalan Numbers. The nth Catalan number is given directly in terms of binomial coefficients by

                                                                               Cn​=n+11​(n2n​)

We will 'code' the Handshake problem later but beforehand let's see Catalan number's applications :

1. Dyck Paths and Acceptable Sequences 

The number of valid parenthesis expressions that consist of $n$ right parentheses and $n$ left parentheses is equal to the $n^\text{th}$ Catalan number. For example, $C_3 = 5$ and there are 5 ways to create valid expressions with 3 sets of parenthesis:

• ( ) ( ) ( )
• ( ( ) ) ( )
• ( ) ( ( ) )
• ( ( ( ) ) )
• ( ( ) ( ) )
  

2. Restricted random walks:

A man walks $n$ blocks north and $n$ blocks west of his residence. Every day he has $2n$ blocks to walk. How many routes are possible if he never crosses the diagonal line from home to office?

Clearly, each acceptable route is either above the diagonal or below the diagonal and both of these paths are symmetric. So we calculate the number of paths below the diagonal and multiply it by 2. Each route is a sequence of $n$ northerly blocks and $n$ westerly blocks. We identify west with $+1$ and north with $-1$. Each route corresponds to a sequence $a_1,a_2, \ldots, a_{2n}$ of $n$ copies of $+1$'s and $n$ copies of $-1$'s. But in order for the route not to go above the diagonal, we must have

$a_1+a_2+\cdots+a_k \ge 0$

for $k=1,2, \ldots, 2n$. So the number of acceptable routes above the diagonal equals the $n^\text{th}$ Catalan number, and the total number of acceptable routes is

$2C_n = \frac{2}{(n+1)} \times \frac{(2n)!}{n!n!}.$

The above diagram shows the routes below the diagonal for $n=5$. Notice that the number of such routes is equal to $C_5 = 42$. So the answer is $2\times 42=84.\ _\square$

3. Binary trees:

A rooted binary tree is a tree with one root node, where each node has either zero or two branches descending from it. A node is internal if it has two nodes coming from it. How many rooted binary trees are there with $n$ internal nodes?

This is a good illustration of proving that a sequence equals the Catalan numbers by using the recurrence relation. Let 

$R_n$ be the number of rooted binary trees with $n$ internal nodes. Then $R_0=R_1 = 1$ as in the picture. Now for $n \ge 0,$ suppose there is a rooted binary tree with $n+1$ internal nodes. The root node is internal. There are $k$ internal nodes on the left and $n-k$ internal nodes on the right, for some $k.$ Looking at the left and right sides gives two rooted binary trees with $k$ and $n-k$ internal nodes, respectively. So

$$R_{n+1} = \sum_{k=0}^n R_kR_{n-k},

which is the same recurrence relation as the Catalan numbers. So $R_n = C_n$ for all $n.$

4. Polygon triangulations:

How many ways are there to cut an $(n+2)$-gon into $n$ triangles, by drawing $n-1$ non-crossing lines between vertices of the polygon?

Let $T_n$ be the number of such triangulations, and define $T_0 = 1$. Consider $T_{n+1}$, which counts triangulations of an $(n+3)$-gon. The idea is to pick an edge of that $(n+3)$-gon and classify triangulations by which triangle that edge ends up in.

Number the vertices $v_1, v_2, \ldots, v_{n+3}$. Suppose our edge is $v_1v_2$. If the triangle this edge ends up in is $v_1v_2v_k$, then this triangle splits the polygon into two remaining polygons that must be triangulated.

• If $k = 3$, then what is left is an $(n+2)$-gon. The number of triangulations like this is $T_0 T_n$.
• If $k=4$, there is a triangle $v_2v_3v_4$ on one side and an $(n+1)$-gon on the other side. The number of triangulations like this is $T_1 T_{n-1}$.
• If $k = 5$, there is a quadrilateral $v_2v_3v_4v_5$ on one side and an $n$-gon on the other side. The number of triangulations like this is $T_2 T_{n-2}$.

Proceeding in this way,

$$T_{n+1} = T_0T_n + T_1T_{n-1} + \cdots + T_n T_0.

Also $T_0 = 1$. This is the same recurrence relation and initial condition that the Catalan numbers satisfy, so it must be the case that $T_n = C_n$ for all $n$. 

##########################################################################

Let's rewrite the main recursive equation of Catalan numbers and search for a pattern.

Equation is : 

                                         Cn+1​ = C0​Cn​ + C1​Cn−1​ + ⋯ + Cn​C0​ = k=0∑n​Ck ​Cn−k

We can see that it has mirror image part of itself, for instance 'C0Cn
' have its mirror part 'Cn​C0' at the end, same follows for others, from this mirror part idea, we can actually find the nth Catalan number from previous values [ Insight of Dynamic programming ]

Let's suppose we already found, first three numbers of Catalan sequence :
1, 2, 5. Write them in vertical order and rewriting the same column again next to it.

1    1

2    2

5    5

Connect them in this fashion:

1     1

  \ /
2--\--2

  / \
5     5

'1' is connected with '5'
'2' is connected with '2'
'5' is connected with '1'

for getting the 4th Catalan number we can multiply these pairs and further add them, i.e
 C(4) = 1*5 + 2*2 + 5*1 = 14

Code for finding nth Catalan Number 

Recursive approach :

Time complexity : Exponential

Further improving this, 

Dynamic Programming solution :

Time Complexity : O(n^2)

Again further optimising and using 

Binomial Coefficient solution:

$Time\; Complexity\; :\; O(n)$

$So\; let\text{'}s\; back\; to\; our\; main\; problem\; ,$

$\text{'}Handshake\; problem\text{'}\; where\; N\; people\; where$

$given\; so,$there we will find (n/2)th Catalan 

number.(here : using DP solution)

       

As many companies like Amazon have asked questions based on this topic : 

Handshake Problem

Bell Numbers