The Longest Increasing Sub-sequence problem is to find a sub-sequence of a given sequence in which the sub-sequence's elements are in sorted order, lowest to highest, and in which the sub-sequence is as long as possible. This sub-sequence is not necessarily contiguous, or unique. Longest increasing sub-sequences are studied in the context of various disciplines related to mathematics, including algorithms, random matrix theory, representation theory, and physics.

Like example :

Input : arr[] = {50, 3, 10, 7, 40, 80}
Output : Length of LIS = 4
The longest increasing sub-sequence is {3, 7, 40, 80}

Here for our input Array, we will divide our main problem into smaller sub-problems, like we will create a new array named(dp[]), in which we will pre-compute longest increasing sub-sequence up-to index 'i' in dp[i].

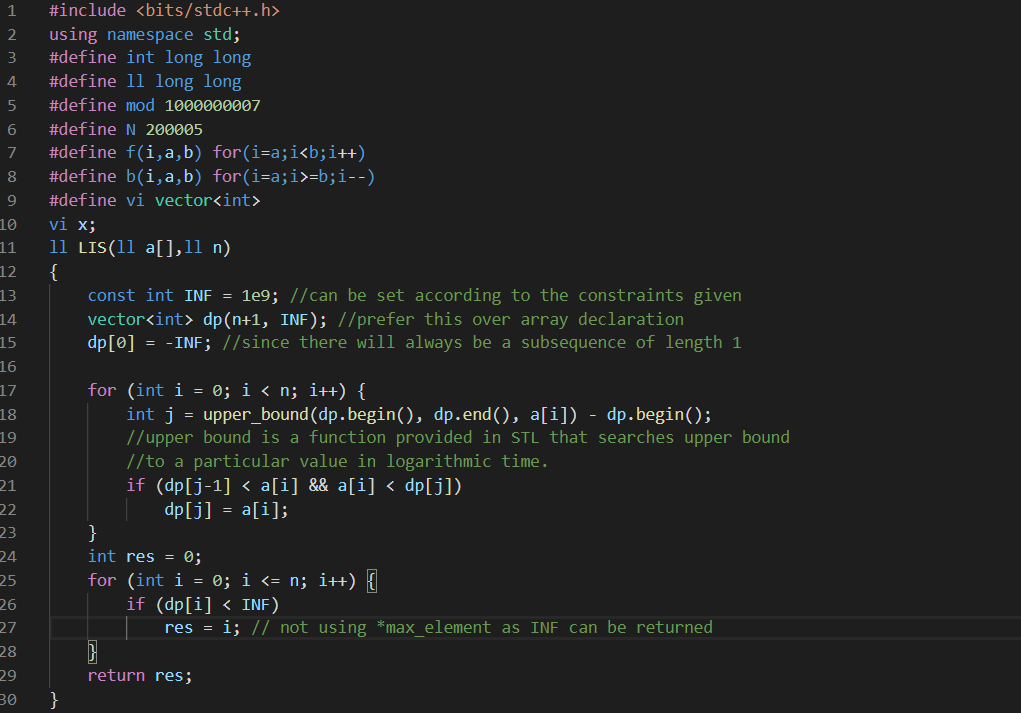
Lets see the code, follow the comments :)

With the help of dp[] array, we get every longest increasing sub-sequence up-to every particular index 'i'.

Here 'best_ans' will be the maximum element of our dp array.

As first 'For' loop will run upto 'n' and whole nested 'For' loop will run for

1 + 2 + 3 .......n values
which will be n*(n+1)/2 i.e

Time Complexity of the above code will be O(n^2)

We can improve this by removing the inner loop and executing " Binary Search ( Complexity of BS : O(log n) ),
so overall complexity will be O(n*log n). While implementing this logic, this time, dp[i] will be the element at which a sequence of length 'i' terminates. Following is the implementation in code: